1. 문제 설명
지나다니는 길을 'O', 장애물을 'X'로 나타낸 직사각형 격자 모양의 공원에서 로봇 강아지가 산책을 하려합니다. 산책은 로봇 강아지에 미리 입력된 명령에 따라 진행하며, 명령은 다음과 같은 형식으로 주어집니다.
["방향 거리", "방향 거리" … ]
예를 들어 "E 5"는 로봇 강아지가 현재 위치에서 동쪽으로 5칸 이동했다는 의미입니다. 로봇 강아지는 명령을 수행하기 전에 다음 두 가지를 먼저 확인합니다.
주어진 방향으로 이동할 때 공원을 벗어나는지 확인합니다.
주어진 방향으로 이동 중 장애물을 만나는지 확인합니다.
위 두 가지중 어느 하나라도 해당된다면, 로봇 강아지는 해당 명령을 무시하고 다음 명령을 수행합니다.
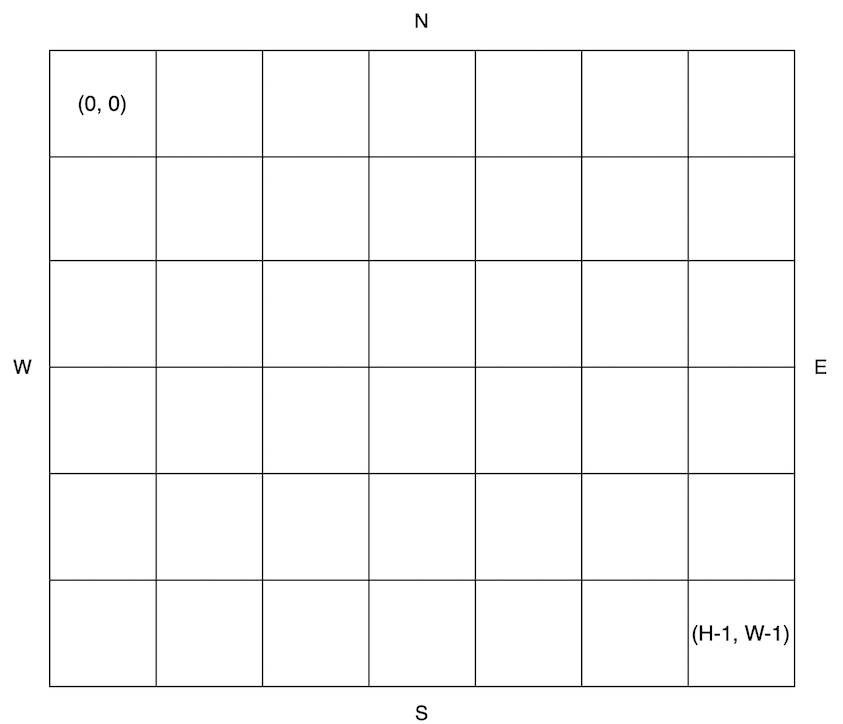
공원의 가로 길이가 W, 세로 길이가 H라고 할 때, 공원의 좌측 상단의 좌표는 (0, 0), 우측 하단의 좌표는 (H - 1, W - 1) 입니다.
공원을 나타내는 문자열 배열 park, 로봇 강아지가 수행할 명령이 담긴 문자열 배열 routes가 매개변수로 주어질 때, 로봇 강아지가 모든 명령을 수행 후 놓인 위치를 [세로 방향 좌표, 가로 방향 좌표] 순으로 배열에 담아 return 하도록 solution 함수를 완성해주세요.
- 제한 조건
-
- 3 ≤ park의 길이 ≤ 50
- 3 ≤ park[i]의 길이 ≤ 50
- park[i]는 다음 문자들로 이루어져 있으며 시작지점은 하나만 주어집니다.
- S : 시작 지점
- O : 이동 가능한 통로
- X : 장애물
- park는 직사각형 모양입니다.
- park[i]는 다음 문자들로 이루어져 있으며 시작지점은 하나만 주어집니다.
- 3 ≤ park[i]의 길이 ≤ 50
- 1 ≤ routes의 길이 ≤ 50
- routes의 각 원소는 로봇 강아지가 수행할 명령어를 나타냅니다.
- 로봇 강아지는 routes의 첫 번째 원소부터 순서대로 명령을 수행합니다.
- routes의 원소는 "op n"과 같은 구조로 이루어져 있으며, op는 이동할 방향, n은 이동할 칸의 수를 의미합니다.
- op는 다음 네 가지중 하나로 이루어져 있습니다.
- N : 북쪽으로 주어진 칸만큼 이동합니다.
- S : 남쪽으로 주어진 칸만큼 이동합니다.
- W : 서쪽으로 주어진 칸만큼 이동합니다.
- E : 동쪽으로 주어진 칸만큼 이동합니다.
- 1 ≤ n ≤ 9
- op는 다음 네 가지중 하나로 이루어져 있습니다.
- 3 ≤ park의 길이 ≤ 50
2. 풀이 코드
#include <string>
#include <vector>
#include <map>
using namespace std;
vector<int> solution(vector<string> park, vector<string> routes) {
vector<int> answer;
// 가로 세로 최대 지점
int MAX_ROW = park.size();
int MAX_COL = park[0].length();
int x = 0;
int y = 0;
// 스타트 지점 찾기
for (int i = 0; i < MAX_ROW; i++)
{
string s = park[i];
for (int j = 0; j < MAX_COL; j++)
{
if (s[j] == 'S')
{
y = i;
x = j;
break;
}
}
}
// 동 남 서 북
int dx[4] = {1,0,-1,0};
int dy[4] = {0,1,0,-1};
map<char, int> dir_map = { {'E', 0}, {'S', 1}, {'W', 2}, {'N', 3}};
for (string route : routes)
{
char dir = route[0];
int move = route[2] - '0';
int newX = x;
int newY = y;
while (move--)
{
newX += dx[dir_map[dir]];
newY += dy[dir_map[dir]];
// 최대 범위 체크
if (newY < 0 || newY >= MAX_ROW || newX < 0 || newX >= MAX_COL)
{
break;
}
// 장애물 있는지
if (park[newY][newX] == 'X')
{
break;
}
}
if (move < 0)
{
x = newX;
y = newY;
}
}
answer.push_back(y);
answer.push_back(x);
return answer;
}
int main()
{
solution({"SOO", "OOO", "OOO"}, {"E 2", "S 2", "W 1"});
}
3. 정리
- H: 공원의 행 수
- W: 공원의 열 수
- R: routes의 길이 (명령 개수)
- M: 명령당 최대 이동 거리 (평균적으로는 작지만, 최악에는 R × M이 될 수 있음)
전체 시간 복잡도는 O(H × W + R × M)
출처 : https://school.programmers.co.kr/learn/courses/30/lessons/172928
'Algorithm' 카테고리의 다른 글
| [프로그래머스] 덧칠하기 (0) | 2025.04.14 |
|---|---|
| [프로그래머스] 바탕화면 정리 (0) | 2025.04.10 |
| [프로그래머스] 추억 점수 (0) | 2025.04.08 |
| [프로그래머스] 달리기 경주 (0) | 2025.04.08 |
| [자료구조] 큐 (0) | 2025.04.02 |